Développement limité ordre 2

Le régime n°en France. Vous avez juste à renseigner la fonction voulue et en quel point vous voulez effectuer le développement limité. Le développement limité ainsi que sa représentation graphique sera affiché ci-dessous. En simplifiant cette équation, on obtient : avec.

Comme, nous avons bien trouvé un développement limité. Développement limité2. SoitI unintervalleetf :I ! On dit que f admet un développement limité à l’. DL de en à l’ordre 3. Correction: en à l’ordre 2. Comme le dénominateur admet pour limite en, on écrit les développements limités du numérateur et du dénominateur à l’ordre 2. Enjoy the videos and music you love, upload original content, and share it all with friends, family, and the world on.

Montrer que est prolongeable par continuité en =0. Autre méthode en utilisant des développements limités connus : Cette méthode est de loin la plus rapide et souvent la plus utilisée. Un développement limité est unique en cas d’existence ou encore on peut identifier les coefficients de deux développements limités égaux. On obtient ainsi les développements suivants, que vous devrez connaître par c ur.

DL, unicité des coefficients, troncature. On justifiera le choix de l’ ordre auquel on commence les calculs, et on détaillera les calculs intermédiaires). AM Maths 4views.

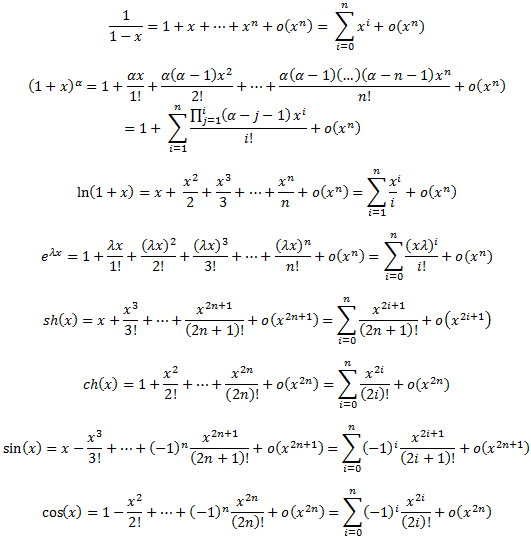
Cours maths sup, prépa HEC. Forum de mathématiques. DL) d’ ordre n en d’une fonction admettant en ce point une dérivée d’ ordre n, est : On notera. Calculs de développements limités ( ). Si la fonction n’est pas définie ou n’admet pas une dérivée.

Déterminer le développement limité. R, une fontion dérivable.

Si f0est dérivable, on note f00ou f( ) la dérivée de f0et on l’appelle dérivée seconde de f. Si f est n-fois dérivable, on note f(n) la dérivée n-ième de f. Applications `a la recherche des limites Les d´eveloppements limit´es permettent de remplacer une fonction par une fonction polynˆome plus simple et de lever une possible ind´etermination. D’une fa¸con g´en´erale, une fonction f(x), quand x �. Ce développement limité se trouve en cherchant un D. Composition si u possède un D. En utilisant la relation fonctionnelle entre tangente, sinus et cosinus.

Exemples Exemple 2. Justifier que f admet un développement limité n’importe quel ordre en 0et calculer a0. Donnerledéveloppementlimitéenx àl’ordrendesfonctions. Les développements limités ci-dessous sont valables quand x tend vers et uniquement dans ce cas.

Tous dépend des cas. Alors que, pour calculer une limite de quotient par exemple, il ne faut pas que le développement limité annule un des deux quotients. Université Savoie Mont Blanc.

Analyse (MATH202) Année académique. Connecte-toi ou inscris-toi pour poster des commentaires. On peut aussi mettre un terme en facteur.