Toutes les limites usuelles pdf

Une gestion moins chère, plus efficace, plus conviviale. Quelques rappels Théorème. LIMITES – EXERCICES CORRIGES Exercice n°1.

Tableaux des primitives usuelles Ce qui est affirmé sans preuve peut être nié sans preuve. La deuxième forme peut servir à dériver la fonction ou à en calculer les limites. Leurs courbes admettent alors l’axe des abscisses comme asymptote horizontale. Développements limités usuels en Les développements limités usuels suivants sont à connaître par coeur!

Nombres dérivés Les limites suivantes sont fournies dans le cours. Elles fournissent toutes un nombre. Limites et Equivalents 1. Par exemple, les fonctions f(x)=x.

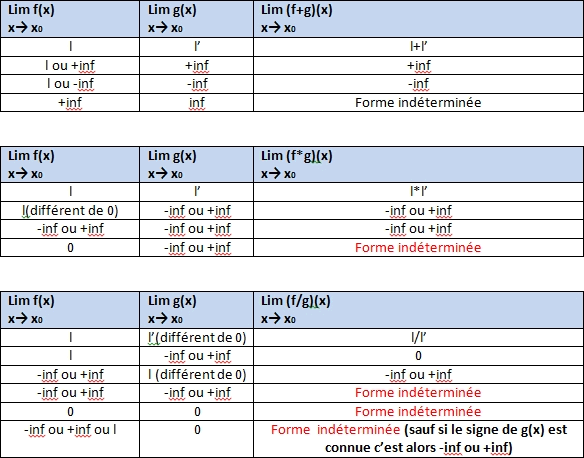
Définition et notations Définition Notations Soit f une fonction définie sur un intervalle ouvert contenant a. Elle peut ne pas être définie en a. Comment calculer des limites aux points qui annulent le dénominateur ? Calculer la valeur prise par le numérateur. Si elle est différente dela limite est infinie.

Etudier alors le signe du dénominateur. FORMULAIRE Dans tout ce formulaire on ne parle pas du domaine de d´efinition de la formule : par exemple √ a sous-entend a n ∈ N∗, k est une constante. Attention, comme nous le verrons en exercice, toutes les fonctions n’admettent pas forcément une limite finie en tout point de leur ensemble de définition.

Dans la plupart des cas on ne connaîtra pas ce c. Mais ce théorème permet d’encadrer le reste. Ceci s’exprime par le corollaire suivant : Corollaire 1. Dire que lafonction f apour limite leréel ℓena signifie que tout intervalle ouvert contenant ℓcontient toutes les valeurs de f(x)pour x suffisamment proche de a. Et bien cette limite n’existe pas, il n’y a qu’à penser à la courbe de la fonction cosinus (en gros des vagues) pour voir que la fonction ne tend vers rien du tout.

Les fonctions exponentielle exp : R! Intérêt des limites Comme on l’a vu, les théorèmes sur les limites sont simples car ils sont très logiques, on peut les retrouver facilement si on les a oubliés. Soit une fonction définie sur un intervalle.

On écrit alors que. Vive le syndic libre. Fonctions usuelles - trigonom etrie - nombres complexes Fonctions usuelles. Alors, f possède une limite en xsi, et seulement si, f possède une limite à gauche, une limite à droite et si ces deux limites sont égales à f(x0).

Ce r´esultat sera essentiel dans la plupart des d´emonstrations de ce document. En effet la plupart des fonctions usuelles sont continues sur leur domaine de définition.

Paire, impaire, rien du tout ? La capacité de détection constitue l’une des caractéristiques fondamentales d’une méthode d’analyse. La recherche de traces de polluants chimiques dans l’environnement ou dans les produits alimentaires a pris, ces dernières années, une importance toute particulière. Pour ces raisons, les capacités de détection doivent être évaluées de manière rigoureuse et selon un.

Télécharger liste verbes usuels gratuitement, liste de documents et de fichiers pdf gratuits sur liste verbes usuels. Montrer que et sont définies pour tout. Tracer le graphe de.

Allez à : Correction exercice Exercice 8. Toutes ces propriétés sont très faciles à démontrerà l’aide de simples calculs de limites. Dérivées et primitives Tale STI2D 1.